Nas últimas semanas, um post do blog definiu os conceitos de rigidez e resistência utilizando um diagrama de tensão e deformação obtido a partir de um ensaio de tração. É muito frequente também dizer que o uso de materiais de núcleo aumentam a rigidez de painéis laminados.
A rigidez que tem um aumento significativo quando se utiliza materiais de núcleo é a rigidez à flexão. A flexão é causada quando um painel apoiado em suas laterais recebe uma carga normal a sua superfície, fazendo com que se deforme de uma maneira que uma das faces esteja submetida à tração, a face oposta à compressão e que a parte central esteja submetida a uma carga de cisalhamento. Esse tipo de carregamento é muito comum no fundo de embarcações como lanchas, por exemplo, que são frequentemente submetidos à pressão hidrodinâmica.
A rigidez, ou a resistência de uma viga à deformação por esse esforço, pode ser calculada como o produto do módulo de elasticidade do material que compõe a estrutura com o segundo momento de inércia da seção transversal, ou seja:
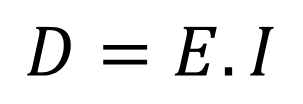
Enquanto o módulo de elasticidade é uma propriedade do material, o momento de inércia da seção transversal é uma característica que varia em função da geometria da estrutura. Como um exemplo, é possível considerar o painel de laminado sólido apresentado na Figura 1.
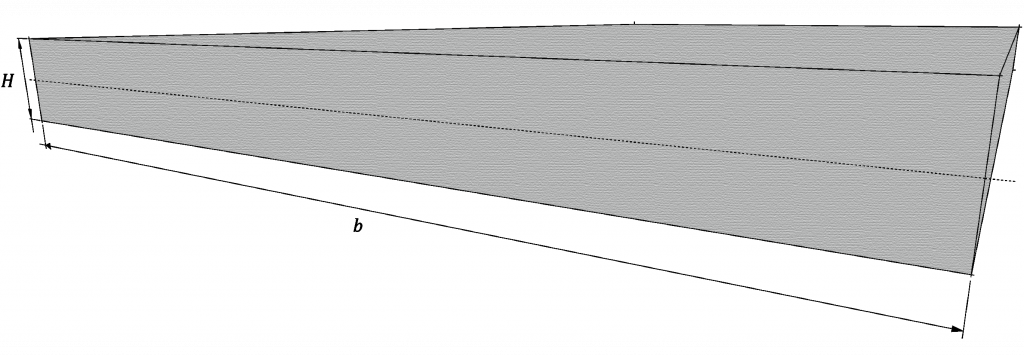
Nesse caso, é possível calcular a rigidez D1 do painel sólido com as dimensões indicadas na figura por meio da equação:
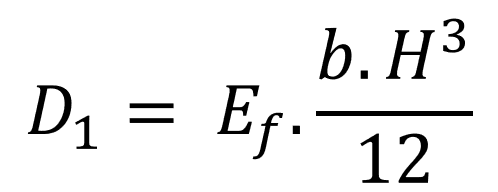
Onde Ef representa o módulo de elasticidade do composto, enquanto b é a largura do painel e H é a espessura. É possível observar que a rigidez à flexão é função do cubo da variável H do painel, o que significa que aumentar a espessura aumenta significativamente essa propriedade.
Aumentar a espessura de laminados sólidos é uma tarefa complicada que pode ser realizada aumentando o teor de resina ou aumentando o número de camadas de fibra. Como visto no post sobre micromecânica, aumentar o teor de resina prejudica muito as propriedades mecânicas do laminado, além de criar maior possibilidade de formação de vazios e aumentar o peso da estrutura. Por sua vez, aumentar o número de camadas de fibra torna o laminado mais caro, mais pesado e superdimensionado para tração sem de fato ter um aumento significativo de espessura.
A melhor solução para esse problema é aumentar a espessura do painel utilizando núcleos de baixa densidade. Para comparação, enquanto um laminado de sólido de fibra de vidro tem 1870 kg/m³, os núcleos de PVC possuem de 40 a 320 kg/m³ sendo que a maior parte das espumas utilizadas para construção náutica variam entre 60 kg/m³ e 130 kg/m.
Podemos utilizar a lógica das equações anteriores para estimar quanto que a inserção de um material de núcleo aumenta a rigidez de um painel sandwich como o ilustrado na Figura 2.
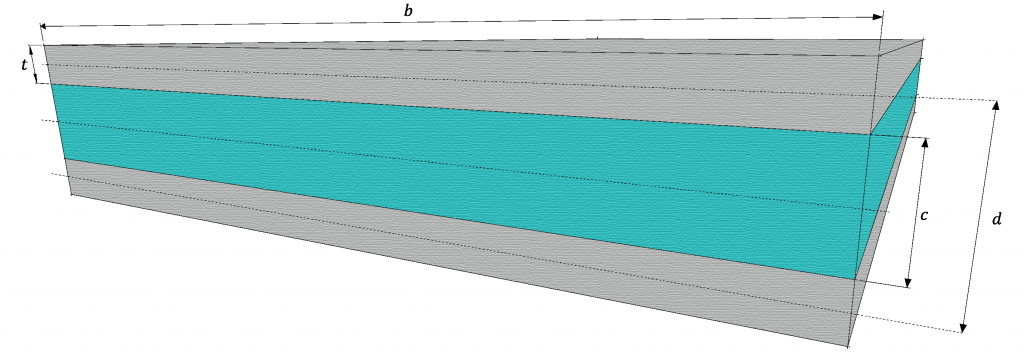
A rigidez D desse painel pode ser calculada a partir da soma das rigidezes das diferentes partes medidas a partir do eixo central da seção transversal, ou seja:
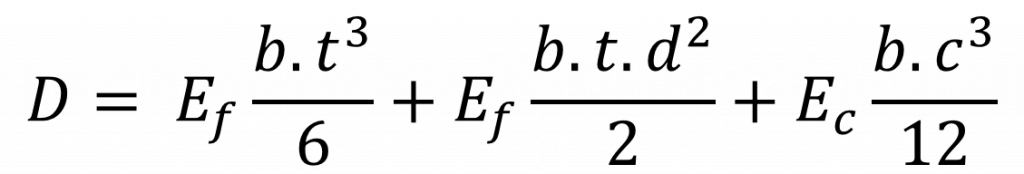
Onde Ec é o módulo de elasticidade do material de núcleo. O primeiro termo da equação diz respeito à rigidez das faces em relação aos seus próprios eixos centrais e pode ser desprezado quando a seguinte condição for satisfeita:
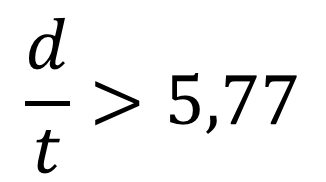
Já o segundo termo computa a transposição do cálculo do segundo momento de inércia das faces para o eixo central do núcleo sandwich. O terceiro termo é o cálculo da rigidez do núcleo em relação ao seu próprio eixo central e pode ser desprezado quando a seguinte expressão for verdade:
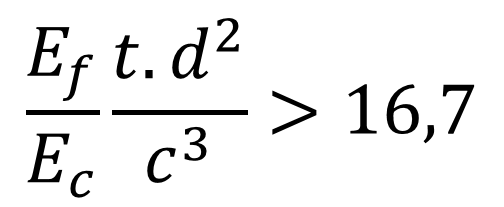
Dessa forma, o cálculo da rigidez de um painel sandwich pode ser realizado a partir da equação:
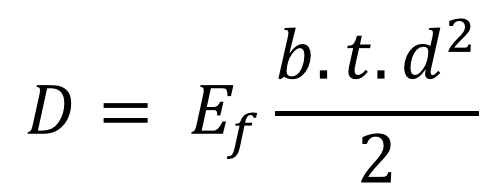
Que finalmente permite a avaliação do quanto o aumento da espessura pela inserção de um material de núcleo influencia a rigidez do painel. A Figura 3 mostra um painel cujas faces são compostas por metade da espessura do painel sólido da Figura 1, com um núcleo de espessura c = H.
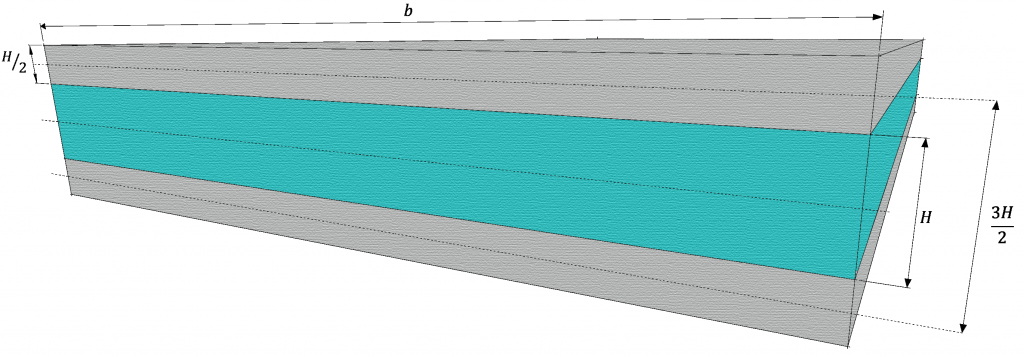
A espessura da faces desse painel é de t = H/2 e a distância entre as linhas de centro das faces é de d = 3H/2. Dessa forma, a rigidez do painel pode ser calculada como:
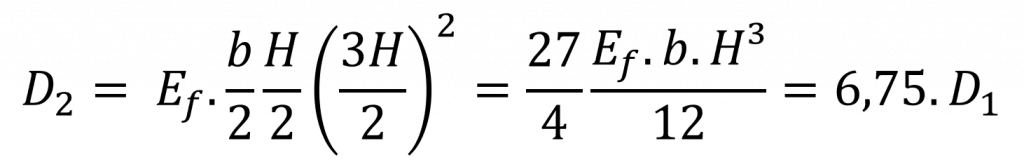
A Figura 4 mostra um painel sandwich cuja espessura é duas vezes maior que a do painel da figura anterior, então, c = 3H. A espessura das faces permanece t = H/2 e, por isso, a distância entre as faces é d = 7H/2.
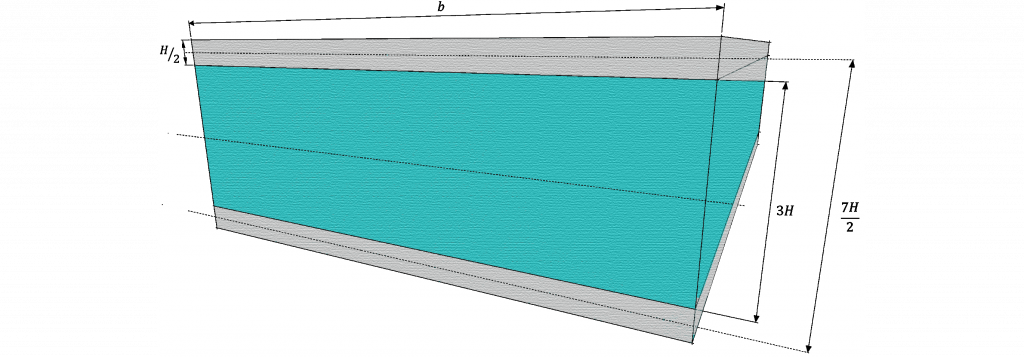
A rigidez desse painel pode ser calculada como:
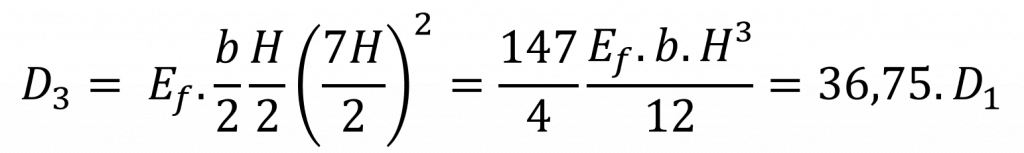
Ou seja, multiplicando a espessura de um painel em duas vezes pela inserção de um material de núcleo, a rigidez aumenta 6,75 vezes. Quando a espessura quadruplica, a rigidez aumenta 36,75 vezes. O aumento de espessura não representa um aumento muito significativo de peso, o que torna a estrutura muito mais eficiente.



francisco bittar disse:
Notei que em alguns veleiros pequenos o casco é feito de um laminado sólido e o convés é em sandwich. Porque é dada essa prioridade para o convés? faria sentido nesses casos de embarcações pequenas fazer ambas as partes em sandwich?
Barracuda Composites disse:
Olá, Francisco
Por questões de estabilidade e conforto durante a navegação, é interessante que o centro de gravidade da embarcação esteja sempre o mais baixo possível em relação à linha de fundo do casco. Então sempre existem esforços para fazer com que conveses e casarias sejam mais leves, por isso pode acontecer de conveses serem fabricados com estrutura sandwichs.
Como discutimos bastante aqui no blog, existem diversas vantagens relacionadas à construção sandwich de embarcações, principalmente com núcleos de espuma PVC. Algumas são a diminuição do peso e aumento da durabilidade da estrutura, independentemente do tamanho da embarcação.